إزاي عرفنا المسافة بين الأرض الشمس؟

لو جيت تفكر في قياس المسافة بينا وبين الشمس هتكتشف إن الموضوع مُعقد جدًا، مفيش أي وسيلة قياس من الوسائل التقليدية اللي بنستخدمها هتنفع لحل الموضوع؛ لأن في الطبيعي لو عاوز تعرف المسافة بين أي نقطتين، كل اللي عليك إنك تجيب مسطرة أو شريط قياس وتفرده بينهم وبمجرد قراءتك للأرقام الموجودة على الشريط هتقدر فورًا تعرف المسافة بين النقطتين، الموضوع بسيط وغاية في السهولة؛ بس ده نظرًا لإن النقطتين بالفعل موجودين قدامك، قادر تلمسهم وقادر كمان إنك تتحرك بينهم.
لكن مع الشمس الموضوع مُختلف تمامًا، الشمس بعيدة عننا جدًا، وبيفصل بينا وبينها مساحة ضخمة من الفراغ، وبالتالي طُرق القياس التقليدية مش هتنفع معاها إطلاقًا.

البداية

المسافة بينا وبين الشمس هي تحديدًا 149 مليون كيلومتر تقريبًا، المُدهش في الموضوع إن الجملة البسيطة اللي قولناها في كام ثانية دي إستغرقت من البشر مئات إن لم يكُن آلاف السنين؛ الموضوع بدأ في اليونان، وتحديدًا على إيد شخص يُدعى (أرُسطُرْخُسْ Aristarchus of Samos)، أرسطرخس هو عالم فلك ورياضيات يوناني عاش في الفترة بين عام 310 قبل الميلاد إلى عام 230 قبل الميلاد، وكان له نظرة مختلفة شوية لشكل السماء والفضاء بخلاف الأشخاص اللي كانوا موجودين في عصره، كان شايف إن الشمس هي مركز كل شئ، وإن الأرض وباقي الكواكب بيدوروا حواليها بإنتظام، والفِكر ده طبعًا مكنش هو الفكر الشائع وقتها، الشاهد في الموضوع إن أرسطرخس ما إكتفاش بكده، ولكنه كان عاوز يعرف بالتحديد المسافة اللي بين الأرض وبين الشمس، واللي بدوره هيوضح للبشرية حاجات كتير، أهمهم إن الشمس غاية في الضخامة، وإنها بتبان في السماء قرص صغير؛ نظرًا لإنها بعيدة عننا جدًا، لكنها في الواقع عكس كده تمامًا.
المهم إن أرسطرخس أثناء محاولته لحساب المسافة بين الأرض وبين الشمس، قال أنا محتاج شوية مُعطيات عشان أقدر أقوم بالمُهمة دي، أول حاجة محتاج أعرف قطر القمر؛ وبناءًا عليه احدد المسافة بين الأرض وبين القمر، وبعد كده محتاج أعرف الزاوية بين القمر والأرض والشمس، وبعدين أحطهم داخل مثلث واحد، وأحاول الاقي علاقة بين أضلاع المُثلث ده، وفعلاً أرسطرخس عمل كده بالفعل، وبدأ في أول مُهمة وهي معرفة قطر القمر.
وعشان يعرف قطر القمر إستنى ليوم المفروض هيحصل فيه خسوف كُلي للقمر، وبدأ يحسب الوقت اللي بيستغرقه القمر إبتداءًا من لحظة دخوله في ظل الأرض، ولحد اللحظة اللي بيبدأ يختفي فيها، واللي مُمكن نمثله في الصورة اللي قدامنا بالمسافة رقم 1

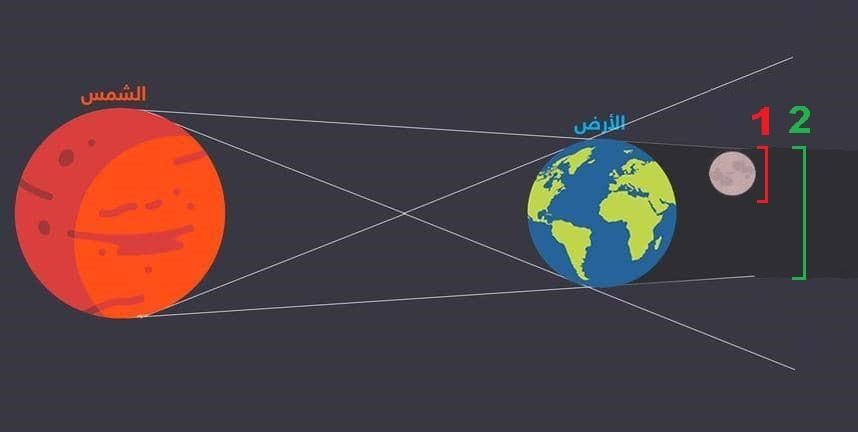
بعد كده بدأ يحسب الزمن الكُلي اللي بيستغرقه القمر أثناء إختفاءه داخل الظل الكامل لـ الأرض، ولحد ما يخرج منه، واللي ممكن نمثله بالمسافة رقم 2، وبالتالي بمعرفة الزمنين، وكذلك بمعلومية محيط كوكب الأرض اللي كان معروف تقريبًا وقتها؛ قدر أرسطرخس في النهاية إنه يحسب محيط القمر بحوالي 13200 كيلو متر، وبكده يبقى نجح في مُهمته الأولى.
بعد كده بقى بدأ أرسطرخس في المرحلة التانية، وهي إنه يحسب المسافة بين كوكب الأرض وبين القمر، وهنا لجأ لـ حيلة لطيفة جدًا وهي إستخدام عملة معدنية دائرية الشكل، والموضوع كان كالتالي:

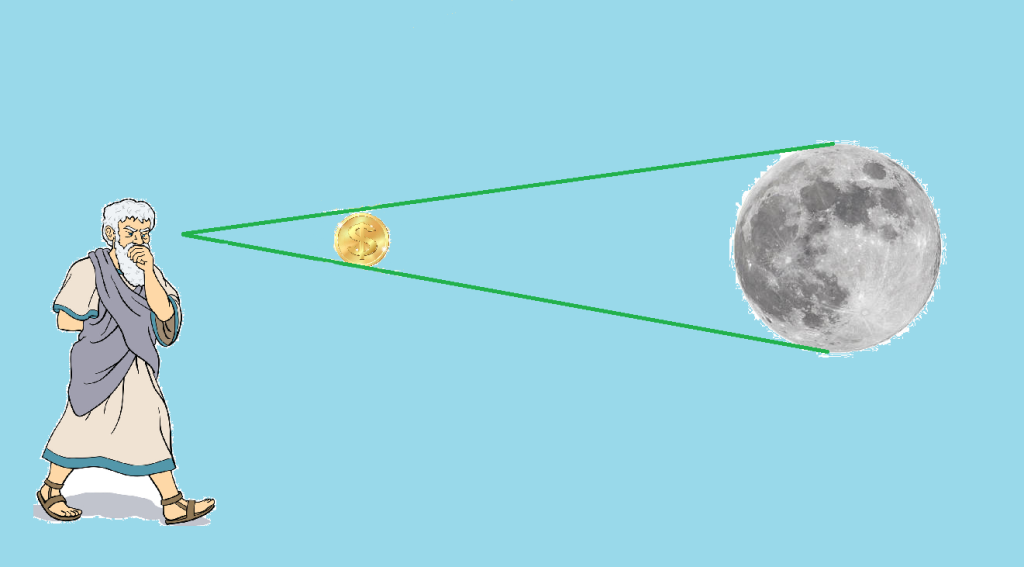
في أحد الليالي اللي القمر فيها كان مُكتمل، ثبِت أرسطرخس العملة في مكانٍ ما، وبدأ يحركها يمين وشمال، وفوق وتحت، لحد ما قِدر يخليها تنطبق على القمر تمامًا من ناحية منظور رؤيته.

وبمجرد إنطباق العُملة على مُحيط القمر بدأ يحسب المسافة بين عينه وبين العُملة، وبناءًا عليه عمل حِسبة بسيطة بإستخدام النِسبة بين المسافة دي ومُحيط العُملة وبين مُحيط القمر اللي كان حاسبُه قبل كده بالفعل؛ وإستنتج إن المسافة بين الأرض وبين القمر تُقدر بحوالي 108 ضعف مُحيط القمر، وقدرها وقتها بإنها تساوي حوالي 374 ألف كيلومِتر، وبكده أنهى أرسطرخس جميع مُعطياته لحساب المسافة بين الأرض وبين الشمس، وفاضله بس شئ أخير، والشئ ده هو إنه يُحط المُعطيات دي كلها داخل مُثلث، ويعرف قياسات زوايا المُثلث، بالإضافة لأحد أضلاعه، وكان بالنسباله أنسب توقيت يقوم فيه بالمُهمة دي، هو الوقت اللي القمر فيه بيكون نصف بدر.

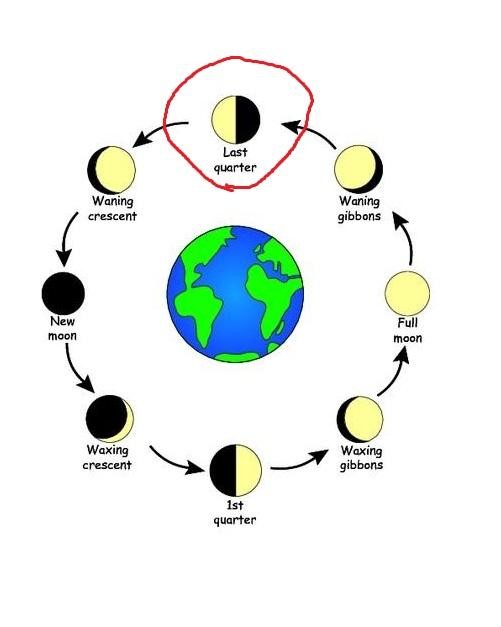
لأن الوقت ده بالتحديد بيبقى القمر فيه في وضع تعامد مع الأرض بالنسبة للشمس، يعني الزاوية رقم 1 اللي في الصور تقدر بـ 90 درجة، أما بقى الزاوية رقم 2 واللي قيمتها 87 درجة، فـ قِدر إنه يحسبها من خلال مُتابعته لدورة القمر وحساب المُدة الزمنية اللي بيستغرقها في الدورة الواحدة، وأخيرًا الزاوية رقم 3 واللي قيمتها تلات درجات، فـ قدر يحسبها بسهولة من خلال قانون مجموع الزوايا الداخلية للمثلث.

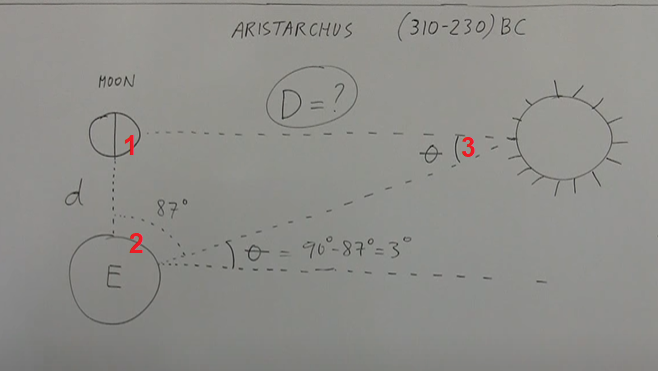
كده معاك مُثلث معلوم فيه ضلع، اللي هو المسافة بين الأرض والقمر، ومعلوم فيه تلات زوايا، وبالتالي هتقدر بسهولة إنك تحسب باقي أطوال أضلاع المُثلث بما فيهم طول المسافة بين الأرض والشمس، وبالفعل قدر أرسطرخس أخيرًا وبعد رحلة طويلة، إنه يستنتج مقدار المسافة بين الأرض والشمس وحسبها بإنها تساوي 20 ضعف المسافة بين الأرض والقمر، يعني حوالي 7.4 مليون كيلومتر.
طبعًا سامعك وإنت بتقول إن الرقم غلط، وبعيد جدًا عن الرقم الحقيقي، لكن برده الراجل كتر خيره جدًا إنه وصل لحد هنا، ولك أن تتخيل إنه مع مرور أكتر من 1500 سنة، ومع ظهور عُلماء نابغين زي الفلكي (نيكولاس كوبرنيكوس Nicolaus Copernicus)، و(تايكو براهي Tycho Brahe)، محدش فيهم قِدر يعدل على الرقم اللي وضعه أرسطرخس من مئات السنين أي تعديل ملموس، أو حتى يبتكر طريقة مشابهة.

ما بعد أرسطرخس

الطريقة اللي إتبعها أرسطرخس في حساب المسافة بين الأرض والشمس، هي طريقة صحيحة رياضيا، بس الخلل اللي حصل عنده كان بيكمُن في عدم الدقة؛ لأن أرسطرخس كان بيسجل كل المشاهدات دي إعتمادًا على عينه المجردة فقط، لحد ما جِه عام 1635 ومع إختراع التليسكوب، قدر عالم الفلك البلجيكي (غودفروا فيندلين godefroy wendelin)، إنه يُجري قياسات أكثر دقة، ولاحظ إن قيمتها مش 3 درجات ولا حاجة زي ما حسبها أرسطرخس في البداية، ولكن قيمتها حوالي ربع درجة فقط، وبالتعويض في المُعادلات السابقة مَرة تانية، إكتشف إن المسافة المفروض تكون 11 ضِعف المسافة اللي حسبها أرسطرخس، يعني حوالي 81 مليون كيلومِتر، طبعًا دي مش هي المسافة الحقيقة بين الأرض والشمس، بس برده الراجل يُشكر؛ لأنه تقريبًا قرب من الرقم الحقيقي بحوالي 60% من قيمته.
ومن بعد غودفروا فيندلين، بدأ العلماء يحاولوا يدوروا على طريقة جديدة تكون أكثر دقة عشان يحسبوا بيها المسافة بين الأرض والشمس، والطريقة السحرية دي كانت من خلال إستغلال عبور كوكب الزهرة من قدام الشمس، كوكب الزهرة بيمر بين الأرض والشمس في دورة ثنائية غريبة جدًا، وبيكون على هيئة نقطة سوداء بتمر من قدام قرص الشمس.

والدورة دي غريبة؛ لأنها بتتكرر كل 243 سنة، وبتتألف من عبورين متتالين بيفصل بينهم 8 سنوات، وبعد 121.5 سنة بيحصل عبورين بيفصل بينهم 8 سنوات، وبعد 105.5 سنة بيحصل عبورين بيفصل بينهم 8 سنوات، وبعدهم يبدأ من الأول، اللفة الغريبة دي بيعود الفضل في اكتشافها 3 أشخاص، الفلكي الألماني يوهانس كيبلر، واللي للأسف مات قبل مرور كوكب الزهرة من قدام قرص الشمس بسنة واحد في عام 1630، وماشافش الحدث اللي تنبأ بيه، ومن بعده الفلكي الإنجليزي (جيريمي هوروكس Jeremiah Horrocks)، وصديقه (وليام كرابتري William Crabtree)، والاتنين دول ما إكتفوش بمراقبة كوكب الزهرة وخلاص، ولكنهم عملوا شئ غريب جدًا.
في وقت مرور كوكب الزهرة في 4 ديسمبر من عام 1639م، وقف جيرمي في مدينة برستون الإنجليزية، وسافر صديقه وليام لمدينة أخرى بالقرب من مانشستر، والاتنين عملوا رصد لكوكب الزهرة في نفس الوقت، واستخدموا تلسكوب بسيط، وجَّهوه ناحية الشمس وحطوا تحت عدسته العينية ورقة صغيرة، بحيث إن صورة الشمس تسقط عليها، وبالتالي يقدروا يشوفوا الحدث بدون ما يعرضوا عنيهم للخطر.

المهم إن جيرمي و وليام بعد ماسجلوا المُشاهدات بتاعتهم، كان الهدف من اللي عملوه إنهم يراقبوا الكوكب وهو على قرص الشمس من مسافتين مختلفتين، وبعدين يحطوا المُشاهدات بتاعتهم مع بعض في ورقة واحدة، وبالتالي يحصلوا على الشكل ده:

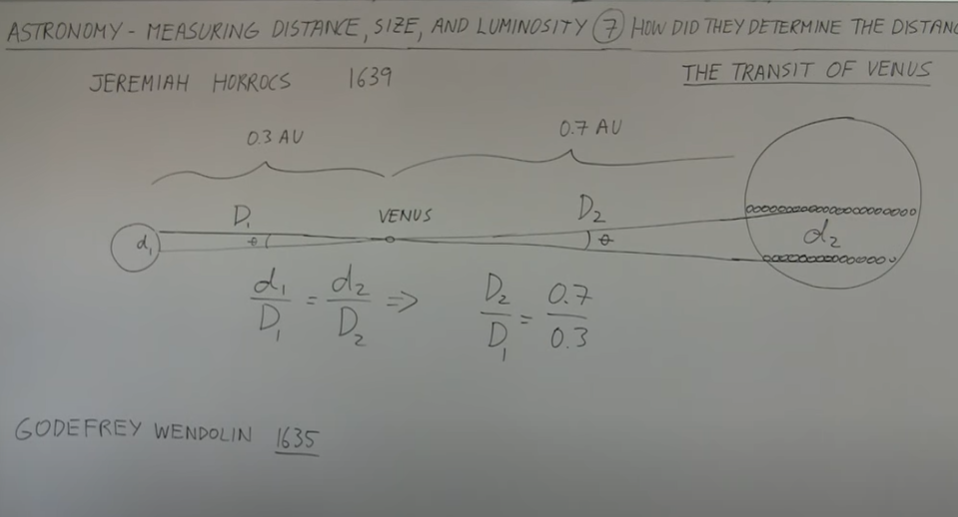
وبدون الدخول في تفاصيل رياضية كتيرة، قدروا انهم في النهاية يستنتجوا المسافة بين كوكب الأرض وبين الشمس، واللي بتقدر بحوالي 144 مليون كيلومتر، ومن بعدهم في عام 1761 وأثناء العبور التالي لكوكب الزهرة، ومع تنبأ الفلكي الروسي (ميخائيل لومونوسوف) إن كوكب الزهرة بيمتلك غلاف جوي، وإن ده لازم يتاخد في الإعتبار أثناء الرصد، قدر الفلكي الإنجليزي (إدموند هالي) إنه يستفيد من عبور كوكب الزهرة في المرة دي لحساب رقم أكثر دقة للمسافة بين الأرض والشمس، وكذلك حجم الشمس نفسها.

القياسات الحديثة للمسافة بين الأرض والشمس

وأخيرًا مع التقدم العلمي وخصوصًا في مجال الفلك، توصل العلماء إن فيه آلية جديدة ممكن يتم إستخدامها لحسابات المسافات في الفضاء، والآلية دي هي مؤشر الشموع المعيارية أو الـ Standard candles، والطريقة دي مُعتمدة بشكل أساسي على معرفة نوع اللمعان اللي بيصدُر من النجوم، واللى وبعمل بعض المُقارنات وبحساب الفترة الزمنية للدورة الواحدة أو التغير الواحد بيقدر العُلماء إنهم يستنتجوا المسافات بينا وبين النجوم بوجه عام، وده زي ما قولنا من خلال الاعتماد على الضوء الصادر منها.